国家公务员考试网提供以下国考行测信息:2018国考备考:盈亏思想---鸡兔同笼在公考中如何快速解题?,更多关于2018,国家,公务员,考试,行测,备考,盈亏思想,国家公务员行测的内容,请关注国家公务员考试频道/湖北人事考试网!咨询电话:027-87870401。国家公务员考试交流群,点击
面试礼包:
 2024国考面试礼包
2024国考面试礼包
面试课程:
 2024国考面试课程
2024国考面试课程
2018国家公务员考试公告已于2017年10月28日发布,笔试时间为2017年12月10日。湖北华图特将2018国考行测备考:盈亏思想---鸡兔同笼在公考中如何快速解题?发布如下,并将持续更新。湖北人事考试网(http://hb.huatu.com/)将及时更新国家公务员、湖北公务员、湖北事业单位等招考资讯。考生敬请关注【2018国考刷题群: 584211943】,咨询电话:027-87870401
相关推荐:国考公告♦报名入口♦职位表♦报考指南 ♦ 国考日程
课程推荐:高频考点♦国考密卷♦国考课程 ♦ 大纲解析会

数量关系一直都是一个“老大难”的问题,究竟怎样才能快速得到正确的选项呢?一般情况下,很多考生都会利用方程来得到答案,可是解方程是一个比较耗时间的事情,特别是有时候因为题目数据比较大或者数据比较繁琐,导致计算速度比较低下,很耗时间。而鸡兔同笼在某些方面简化了计算,提高了计算速度,为小伙伴在考试中争夺了时间,夺取了最后的公考胜利。今天小编给大家带来了盈亏思想---“鸡兔同笼”,那么“鸡兔同笼”在公考中如何快速解题呢?今天给大家一起进行分享。
一、鸡兔同笼的概念
古时候,有一个农民伯伯养了一群鸡和兔子,有一天他跟他的邻居说:“我把我的鸡和兔子关在同一个笼子里,从上面数有36个头,从下面数有120只脚,你猜猜我具体有多少只鸡,有多少只兔子?”这是鸡兔同笼最原始最典型的例子。
二、鸡兔同笼的适用范围
已知两个事物两种属性的指标数及指标总数。
以刚才的概念为例,这里面的两种事物指的是鸡和兔子,两种属性是头和脚。
以后碰到此类问题小伙伴们可以用鸡兔同笼来解决啦!是不是很开心撒!!!——三、鸡兔同笼的解法(也称为假设法)
1、假设全部是其中一种事物,比如假设36个头都是鸡;2、通过假设的事物算出两种属性的具体情况,再根据已知条件和假设的结果得到差值。
比如:假设36个头都是鸡,那么36只鸡有72只脚,但实际上有120只脚,多出了48只脚,说明有兔子存在。
3、根据差值计算出另一种事物的数量。
因为一只兔子比一只鸡多两只脚,所以每多两只脚就多一只兔子,一共多了48只脚,则有兔子48÷2=24只,则鸡有36-24=12只。
四、鸡兔同笼的应用
例:已知鸡兔共有头35,共有脚94,求鸡和兔的个数。
方法一:方程法:(一元一次方程)
设鸡的个数为x,则兔的个数为(35-x),则有2x+4(35-x)=94,解得x=23故有鸡23只,兔12只。
方法二:方程法:(二元一次方程组)
设鸡的个数为x,兔的个数y,
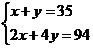
解得
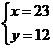
方法三:假设法:
假设全部是鸡,一只鸡两只脚,那么有脚35×2=70,现在有脚94,多出94-70=24脚,那说明一定有兔子的存在,因为一只兔子比一只鸡多出2只脚,所以兔子个数为24÷2=12只,鸡35-12=23只。
通过上述分析,小编给大家总结一个公式
Ⅰ、设鸡求兔:兔数=(总脚数——每只鸡脚数×总只数)÷(每只兔脚数——每只鸡脚数),鸡数=总只数——兔数。
Ⅱ、设兔求鸡:鸡数=(每只兔脚数×总只数——总脚数)÷(每只兔脚数——每只鸡脚数),兔数=总只数——鸡数。
利用上述理论公式
设鸡求兔:兔数=(94-2×35)÷(4-2)=12 鸡数=35-12=23
设兔求鸡:鸡数=(4×35-94)÷(4-2)=23 兔数=35-23=12
【例1】小明负责将某农场的鸡蛋运送到小卖部。按照规定,每送达1枚完整无损的鸡蛋,可得运费0.1元;若有鸡蛋破损,不仅得不到该枚鸡蛋的运费,每破损一枚鸡蛋还要赔偿0.4元。小明10月份共运送鸡蛋25000枚,获得运费2480元。那么,在运送过程中,鸡蛋破损了:( )。
A.20枚 B.30枚C.40枚 D.50枚【解析】C
方法一:方程法
设:鸡蛋破损了x枚,则完整无损的鸡蛋为(25000-x)枚根据运费列出方程式:0.1(25000-x)-0.4x=2480,解得x=40故选C。
方法二:假设法
先判断是否符合鸡兔同笼问题,两种事物是破损鸡蛋和完整无损鸡蛋,两种属性为数量和报酬,然后根据鸡兔同笼的解法步骤解题:
假设25000枚全部是完整无损的鸡蛋,得到假设值和实际值之间的差值。
25000枚完整无损的鸡蛋,得到报酬2500元,但实际只有2480元,相差了20元,说明其中有打破的鸡蛋,计算打破鸡蛋的个数。一个完整无损的鸡蛋与一个破损的鸡蛋报酬的差值是0.1-(-0.4)=0.5元,所以破损的鸡蛋为:
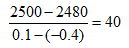
故选C。
【例2】玻璃厂委托运输公司运送400箱玻璃。双方约定:每箱运费30元,如箱中玻璃有破损,那么该箱的运费不支付且运输公司需赔偿损失60元。最终玻璃厂向运输公司共支付9750元,则此次运输中玻璃破损的箱子有:( )。
A.25箱 B.28箱C.27箱 D.32箱【解析】A
方法一:方程法
设破损箱子为x,则无破损的箱子为(400-x)则有:30x-60(400-x)=9750,解得x=25。故选A。
方法二:假设法
先判断是否符合鸡兔同笼问题,两种事物是破损箱子和完整无损箱子,两种属性为数量和报酬,然后根据鸡兔同笼的解法步骤解题:
假设400箱全部是完整无损的箱子,得到假设值和实际值之间的差值。
400箱完整无损的箱子,得到报酬30×400=12000元,但实际只有9750元,相差了2250元,说明其中有打破的箱子,计算破损的箱子个数。一个完整无损的箱子与一个破损的箱子报酬的差值是30-(-60)=90元,所以破损的箱子为:
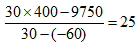
故选A。
【例3】某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位,甲教室每排可坐10人,乙教室每排可坐9人。两教室当月共举办该培训27次,每次培训均座无虚席,当月共培训1290人次。问甲教室当月共举办了多少次这项培训?
A.8 B.10C.12 D.15【解析】D
方法一:方程法
甲教室一次可坐10×5=50人,乙教室一次可坐9×5=45人,设甲教室举办了x次培训,则有: 50x+45(27-x)=1290,解得x=15。故选D。
方法二:假设法
先判断是否符合鸡兔同笼问题,两种事物是甲教室和乙教室,两种属性为培训次数和人数,然后根据鸡兔同笼的解法步骤解题:
假设全部在乙教室培训,乙教室一次可坐9×5=45人,乙教室培训的人次为45×27=1215,实际培训的人次为1940人,假设值和实际值之间的差值为1940-1215=765人。说明其中有人在乙教室培训,计算乙教室培训的人数。甲教室一次培训的人数与乙教室一次培训的人数差值,因为甲教室一次可坐10×5=50人,乙教室一次可坐9×5=45人,两者差值是50-45=5人,所以甲教室培训的场次为:
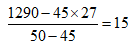
故选D。
鸡兔同笼的题目远远不止这些,这仅仅是几个经典例子,小编希望考生能通过对典型例子的学习,了解到鸡兔同笼的精髓所在,在做其他题目时灵活运用,缩短做题时间,赢得考场的最后胜利,小伙伴们加油。
国家公务员考试网推荐:
(编辑:admin)
![]() 文章来源:湖北华图
文章来源:湖北华图
![]()
![]() 2024国考面试礼包
2024国考面试礼包
![]() 2024国考面试课程
2024国考面试课程

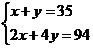 解得
解得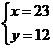
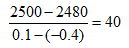 故选C。
故选C。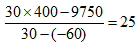 故选A。
故选A。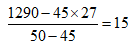 故选D。
故选D。